(1) 天体高度を観測した時の正確な世界時(U)を求める。
世界時＝クロノメ−タ示時＋クロノメ−タ誤差
(2) 世界時を用いて天測暦からE＊，赤緯d，P.P.for Uを求める。
P.P.for Uを計算で求める場合は、次式を使用する。
P.P.for U=(24H-EROT)*U/EROT
EROT=23H56M4.0905S=23.9345H
U:世界時， EROT:地球自転周期
(3) 天体のグリニジ時角HGを求める．HG=U+E＊(U=0H)+P.P.for U
E＊(U=0H)は、当日世界時0時における天体のE値であり、
赤緯d は天体の地位の緯度、-HG は天体の地位の経度になっている。
(4) 推測船位における天体の高度（計算高度）と方位角を求める。
|
AC(ti)
|
=sin-1{sin[d(ti)]･sin(l0)+cos[d(ti)]･cos(l0)･cos[H(ti)]}
| |
Z(ti)
|
=sin-1{cos[d(ti)]･sin[H(ti)]/cos[AC(ti)]}
| |
H(ti)
|
=L0+HG(ti)
| |
AEW
|
=sin-1{sin[d(ti)]/sin(l0)}
|
|
AC(ti)：
|
tiにおける天体の計算高度（推測船位における天体真高度）
| |
Z(ti)：
|
天体方位角
| |
d(ti)：
|
時刻tiにおける天体の赤緯
| |
H(ti)：
|
時刻tiる天体の時角
| |
AEW(ti)：
|
時刻tiにおける天体の東西圏上高度
| |
(l0,L0)：
|
推測船位における緯度，経度
|
＜天体方位角Z の前後に付ける符号を決める＞
(5) 天体の観測高度に測高度改正を行い，真高度AT(tｉ)を求める。
測高度改正は、天測計算表の測高度改正表を用いる。
尚、本システムでは、眼高差については天測計算表に示されている次式を用い、
気差については理科年表に示されている近似式を用いた。
眼高差=-1.776'×H0.5+0.2'×(ta -tw )
H：眼高(m)， ta：気温， tw：水温
(6) 時刻tｉにおける修正差を求める。 I(tｉ)=AT(tｉ)-AC(tｉ)
I(tｉ)：時刻(tｉ)における修正差
AT(tｉ)：天体真高度，AC(tｉ)：天体計算高度
(7) 速力（船速）と航走時間より 1番目の天体を観測してから
2番目の天体を観測するまでの航走距離Distを求める。
(8) 方位角Z(tｉ) ，修正差I(tｉ) を用いて位置の線を作図する。
又、時刻(tｉ)におけるの位置の線L1(tｉ)を針路と航走距離で
転位することにより時刻(t2)における位置の線L1(t2) を得る。
（ 1番目の天体の位置の線を針路と航走距離で平行移動する。）
(9) 図よりD.lat, Depを読み取り，Dep をD.longに変換する。
D.long=Dep/cos(l0) l0：推測船位の緯度
(10)推測船位の緯度，経度にD.lat, D.long を加えて時刻(t2)に
おける天測船位を求める。
l=l0+D.lat L=L0+D.long
(l0,L0)：推測船位の緯度，経度 (l,L)：天測船位の緯度，経度
＜補足＞ 天測位置を計算で求める方法
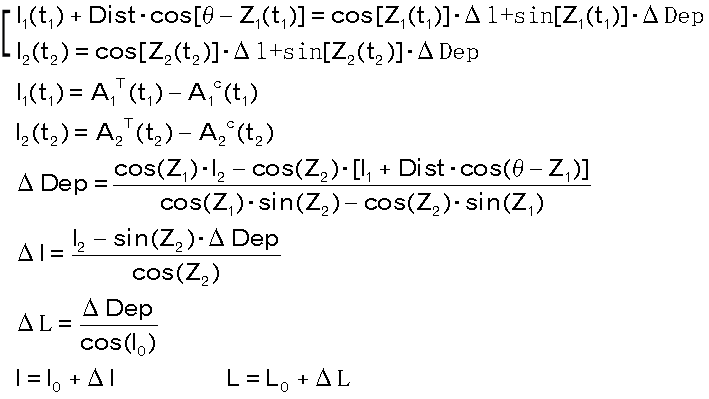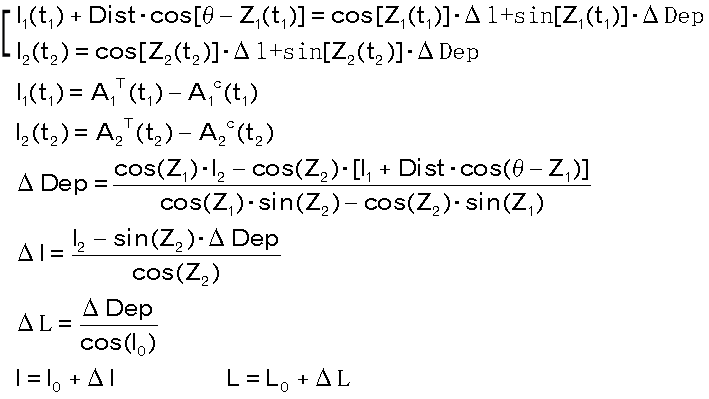AiT(ti)：i番目の天体の時刻(ti)における真高度(i=1〜2)
AiC(ti)：i番目の天体の時刻(ti)における計算高度(i=1〜2)
Zi(ti)：i番目の天体の時刻(ti)における方位角(i=1〜2)
Ii(ti)：i番目の天体の時刻(ti)におけるインターセプト(i=1〜2)
|